3 X 4 5 X 2
ghettoyouths
Nov 15, 2025 · 9 min read
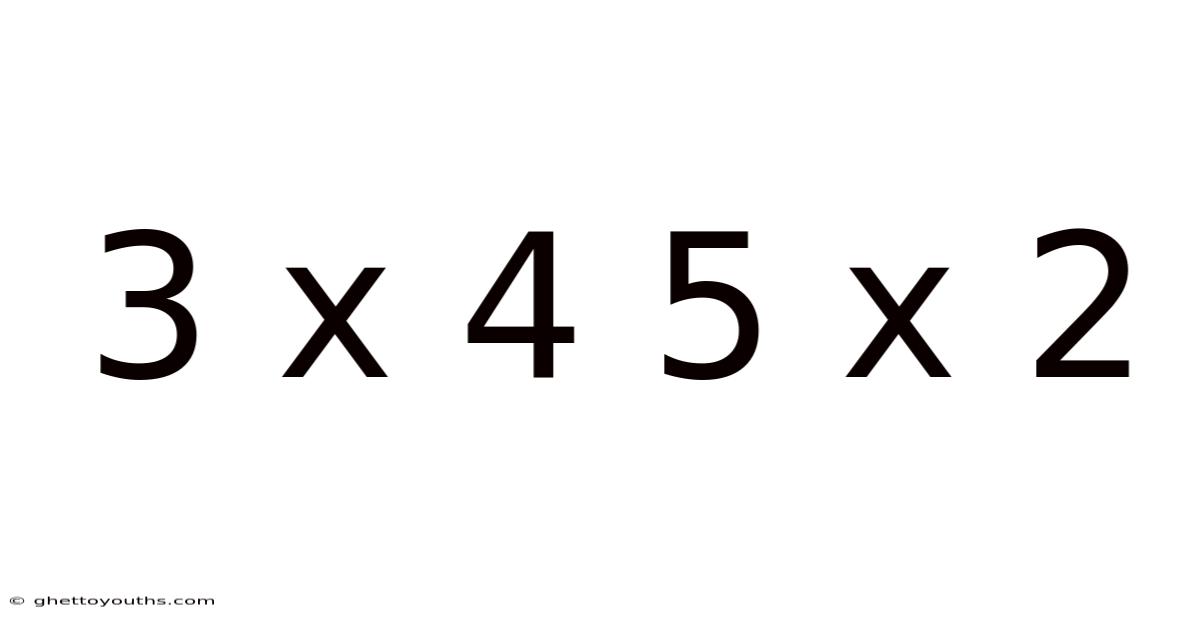
Table of Contents
Let's delve into the seemingly simple yet surprisingly rich world of multiplication, exploring the expressions "3 x 4" and "5 x 2." While they might appear as elementary school arithmetic, these expressions are fundamental building blocks of mathematics, touching upon diverse fields like geometry, computer science, and even everyday problem-solving. Understanding them deeply unlocks a broader comprehension of mathematical principles and their practical applications.
Introduction to Multiplication: More Than Just Times Tables
Multiplication, at its core, is a shorthand way of representing repeated addition. Instead of writing 3 + 3 + 3 + 3, we can simply write 3 x 4, which means "three added to itself four times," or, equivalently, "four added to itself three times." This seemingly small change in notation becomes incredibly powerful when dealing with larger numbers and more complex calculations. It's a cornerstone of arithmetic and acts as a gateway to algebra, calculus, and beyond.
The beauty of multiplication lies not just in its computational efficiency but also in its conceptual elegance. It represents scaling, grouping, and area calculations. Consider arranging objects in a rectangular grid. The total number of objects can be found by multiplying the number of rows by the number of columns. This simple observation connects arithmetic to geometry, a connection that continues to be vital in advanced mathematics.
Unpacking 3 x 4: A Concrete Example
Let's take a closer look at 3 x 4. We can interpret this in several ways:
- Repeated Addition: 3 x 4 = 3 + 3 + 3 + 3 = 12
- Grouping: Imagine you have 4 groups of 3 objects each. The total number of objects is 3 x 4 = 12.
- Rectangular Array: Picture a rectangle with 3 rows and 4 columns. The total number of squares in the rectangle is 3 x 4 = 12.
These different interpretations highlight the versatility of multiplication. It's not just a mechanical process; it's a representation of real-world relationships.
Visualizing 3 x 4: The Power of Representation
Visualizing 3 x 4 can make the concept even more intuitive. Here are a few ways to visualize it:
- Dots: Draw four groups of three dots. Count them. You have 12 dots.
- Arrays: Arrange objects (like coins or candies) in a 3x4 grid. You'll have a rectangular arrangement of 12 objects.
- Number Line: Start at 0 on a number line. Make four jumps of size 3. You'll land on 12.
These visual aids are particularly helpful for young learners, allowing them to grasp the underlying meaning of multiplication before diving into rote memorization of times tables. They provide a concrete foundation that makes abstract concepts more accessible.
Delving into 5 x 2: Another Perspective
Now, let's examine 5 x 2. Similar to 3 x 4, we can interpret this in multiple ways:
- Repeated Addition: 5 x 2 = 5 + 5 = 10
- Grouping: Think of 2 groups with 5 items in each group. The total is 5 x 2 = 10.
- Rectangular Array: Imagine a rectangle with 5 rows and 2 columns. The rectangle contains 5 x 2 = 10 squares.
The key difference between 3 x 4 and 5 x 2 isn't just the numbers involved; it's the perspective it offers on the commutative property of multiplication.
The Commutative Property: Order Doesn't Matter
One of the most important properties of multiplication is the commutative property, which states that the order in which you multiply numbers doesn't affect the result. In other words, a x b = b x a.
Therefore, 3 x 4 = 4 x 3 = 12, and 5 x 2 = 2 x 5 = 10.
This property might seem obvious, but it's crucial for simplifying calculations and understanding algebraic manipulations. Imagine you're trying to calculate the area of a rectangle. It doesn't matter whether you consider the length to be 3 and the width to be 4, or vice versa. The area will always be 12. The commutative property assures us of this.
Applications Beyond Arithmetic: Where Multiplication Shines
While 3 x 4 and 5 x 2 are simple arithmetic problems, the principles of multiplication extend far beyond basic calculations. Here are a few examples:
- Area and Volume: As mentioned earlier, multiplication is fundamental to calculating area and volume. The area of a rectangle is length x width, and the volume of a rectangular prism is length x width x height.
- Scaling Recipes: If a recipe calls for 2 cups of flour and you want to double the recipe, you multiply each ingredient amount by 2.
- Calculating Percentages: Finding 20% of a number involves multiplying the number by 0.20.
- Computer Graphics: In computer graphics, multiplication is used extensively for scaling, rotating, and translating objects. Matrix multiplication is a core operation in 3D graphics pipelines.
- Probability: If you flip a coin twice, the probability of getting heads both times is (1/2) x (1/2) = 1/4.
- Financial Calculations: Calculating simple interest involves multiplying the principal amount by the interest rate and the time period.
These examples demonstrate the pervasive nature of multiplication in various fields. Understanding the fundamentals of multiplication is essential for success in many areas of life.
The Distributive Property: Expanding Our Toolkit
Another important property related to multiplication is the distributive property, which states that a x (b + c) = (a x b) + (a x c). This property allows us to break down complex multiplication problems into simpler ones.
For instance, consider calculating 3 x 14. We can rewrite 14 as 10 + 4. Then, using the distributive property:
3 x 14 = 3 x (10 + 4) = (3 x 10) + (3 x 4) = 30 + 12 = 42
The distributive property is a powerful tool for mental math and is also essential for understanding algebraic expressions.
Multiplication in Different Number Systems
While we've focused on multiplication with whole numbers, the same principles apply to other number systems, such as fractions, decimals, and negative numbers.
- Fractions: Multiplying fractions involves multiplying the numerators and the denominators: (a/b) x (c/d) = (a x c) / (b x d).
- Decimals: Multiplying decimals is similar to multiplying whole numbers, but we need to account for the decimal places.
- Negative Numbers: Multiplying negative numbers follows specific rules: a negative number multiplied by a positive number results in a negative number, while a negative number multiplied by a negative number results in a positive number.
Understanding how multiplication works in different number systems is crucial for advanced mathematical concepts.
Building Blocks for Higher Mathematics
The seemingly simple operations of 3 x 4 and 5 x 2 lay the foundation for more complex mathematical concepts. As students progress through their mathematical education, they'll encounter multiplication in algebra, calculus, and other advanced topics.
- Algebra: Multiplication is used extensively in algebraic expressions and equations. Simplifying expressions, factoring polynomials, and solving equations all rely on the principles of multiplication.
- Calculus: Multiplication is used in derivatives, integrals, and other calculus operations. The product rule and chain rule, for example, are essential tools for differentiating complex functions.
A solid understanding of basic multiplication is essential for success in these higher-level courses. Without it, students may struggle to grasp the more abstract concepts.
Tips & Expert Advice for Mastering Multiplication
Mastering multiplication takes time and practice. Here are some tips and expert advice to help you improve your multiplication skills:
- Memorize Multiplication Tables: Knowing your multiplication tables up to 12 x 12 is essential for quick and accurate calculations. Use flashcards, online games, or other methods to help you memorize them.
- Practice Regularly: The more you practice multiplication, the better you'll become. Set aside some time each day to work on multiplication problems.
- Use Visual Aids: Visual aids can help you understand the concept of multiplication and make it easier to remember. Draw arrays, use number lines, or find other ways to visualize multiplication problems.
- Break Down Problems: Use the distributive property to break down complex multiplication problems into simpler ones. This can make them easier to solve mentally.
- Check Your Work: Always check your work to make sure you haven't made any mistakes. Use a calculator or other methods to verify your answers.
- Understand the Properties: Familiarize yourself with the commutative, associative, and distributive properties of multiplication. Understanding these properties can simplify calculations and provide a deeper understanding of the operation.
- Use Real-World Examples: Look for real-world examples of multiplication to help you understand how it's used in everyday life. This can make learning multiplication more engaging and meaningful.
By following these tips, you can improve your multiplication skills and build a solid foundation for more advanced mathematical concepts.
The Importance of Multiplication in Education
Multiplication is a fundamental skill that's essential for success in mathematics and other fields. It's typically introduced in elementary school, and mastery of multiplication is crucial for progressing to more advanced topics.
Education systems emphasize multiplication because it:
- Develops Number Sense: Understanding multiplication helps children develop a strong sense of number and quantity.
- Prepares for Algebra: Multiplication is a cornerstone of algebra, and students who have mastered multiplication are better prepared for algebraic concepts.
- Enhances Problem-Solving Skills: Multiplication is used in a wide variety of problem-solving situations, from calculating the cost of groceries to designing a building.
- Improves Cognitive Skills: Learning multiplication improves cognitive skills such as memory, attention, and logical reasoning.
Therefore, it's crucial for educators to provide students with ample opportunities to learn and practice multiplication.
FAQ (Frequently Asked Questions)
- Q: What is multiplication?
- A: Multiplication is a mathematical operation that represents repeated addition.
- Q: What is the commutative property of multiplication?
- A: The commutative property states that the order in which you multiply numbers doesn't affect the result (a x b = b x a).
- Q: What is the distributive property of multiplication?
- A: The distributive property states that a x (b + c) = (a x b) + (a x c).
- Q: How can I improve my multiplication skills?
- A: Memorize multiplication tables, practice regularly, use visual aids, break down problems, and check your work.
- Q: Is multiplication important for higher mathematics?
- A: Yes, multiplication is a fundamental skill that's essential for algebra, calculus, and other advanced topics.
Conclusion: Multiplication as a Gateway to Mathematical Understanding
From the simple expressions of 3 x 4 and 5 x 2, we've explored the foundational importance of multiplication. It's more than just memorizing times tables; it's understanding the concept of repeated addition, grouping, scaling, and the relationship between numbers. We've seen how multiplication connects to geometry, algebra, and even computer graphics.
Mastering multiplication is a crucial step in developing a strong foundation in mathematics. By understanding the basic principles and practicing regularly, anyone can improve their multiplication skills and unlock a deeper understanding of the mathematical world.
How do you plan to strengthen your understanding of multiplication, and what areas of math are you excited to explore further with this foundational knowledge?
Latest Posts
Latest Posts
-
Was Ronald Reagan A Good President Reddit
Nov 15, 2025
-
Kohlberg Moral Development Stages By Age
Nov 15, 2025
-
The Difference Between Nominal Gdp And Real Gdp
Nov 15, 2025
-
How To Find The Standard Deviation Of A Binomial Distribution
Nov 15, 2025
-
Which Of These Is Found In The Dorsal Body Cavity
Nov 15, 2025
Related Post
Thank you for visiting our website which covers about 3 X 4 5 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.