Solve For B Ax By C
ghettoyouths
Nov 18, 2025 · 11 min read
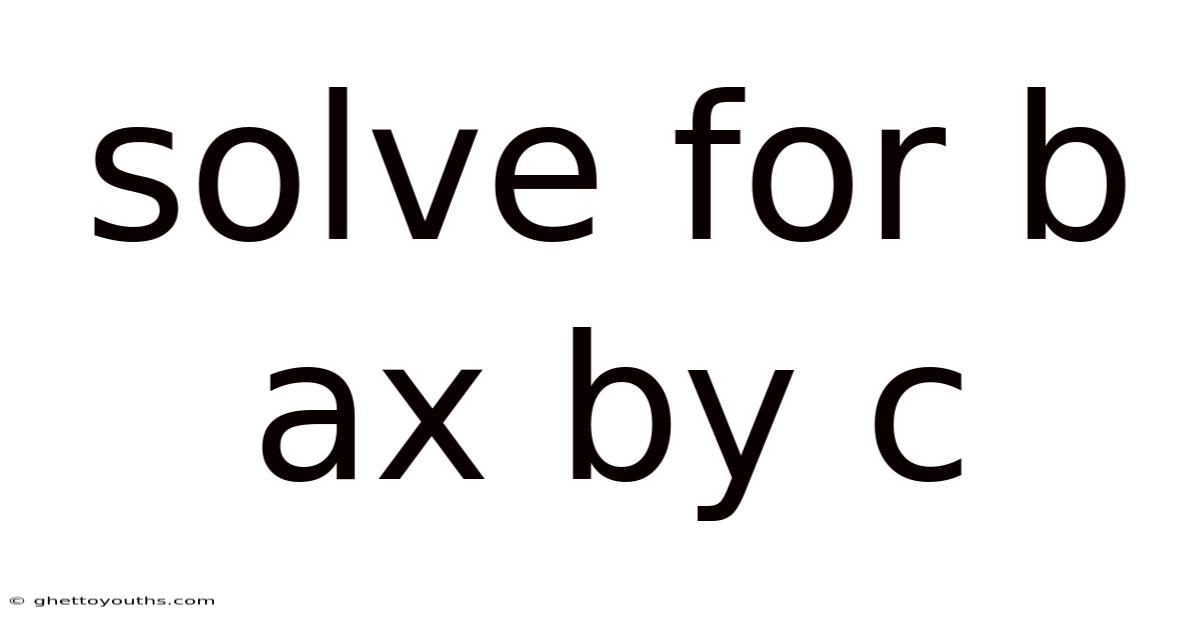
Table of Contents
Alright, let's craft a comprehensive and SEO-friendly article exceeding 2000 words that dives deep into solving for 'b' in the equation "ax + by = c". Here's the structure and content you requested, aimed at educating readers from various backgrounds:
Title: Mastering the Art of Isolating 'b': A Comprehensive Guide to Solving ax + by = c
Introduction
Algebraic equations can seem like daunting puzzles, but they are the foundation of countless scientific and mathematical principles. One of the most common and fundamental linear equations is of the form ax + by = c, where a, b, and c are constants, and x and y are variables. Solving for a specific variable in this equation is a cornerstone skill in algebra. This article focuses specifically on how to isolate and solve for 'b' in this equation, providing a step-by-step guide, practical examples, and advanced insights. Understanding this process is crucial for various applications, from simple problem-solving to complex mathematical modeling.
The ability to manipulate and solve for variables in equations like ax + by = c unlocks the door to a deeper understanding of mathematical relationships. Whether you're a student tackling algebra for the first time or someone looking to refresh their mathematical skills, mastering the technique of isolating 'b' will prove invaluable. This guide will provide you with a clear, concise, and comprehensive approach to tackling this equation with confidence. We'll break down the process into manageable steps, explore real-world examples, and address common pitfalls to ensure a thorough understanding.
Subjudul utama: Understanding the Basics of Linear Equations
Before we dive into solving for 'b', it's crucial to understand the fundamentals of linear equations. A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable. The variables are only raised to the first power (no squares, cubes, etc.), and the equation doesn't contain products of variables. In our equation, ax + by = c, both 'x' and 'y' are variables, while 'a', 'b', and 'c' are constants – fixed values that do not change within the context of a specific problem.
Understanding the role of each component is key. The constants 'a' and 'b' are coefficients that multiply the variables 'x' and 'y', respectively. The constant 'c' represents the constant term on the other side of the equals sign. The goal of solving for a variable, such as 'b', is to isolate it on one side of the equation, expressing it in terms of the other variables and constants. This process involves applying algebraic operations such as addition, subtraction, multiplication, and division while maintaining the equality of the equation.
Comprehensive Overview: Step-by-Step Guide to Isolating 'b'
Here’s a detailed, step-by-step guide to solving for 'b' in the equation ax + by = c:
-
Isolate the term containing 'b': The first step is to isolate the term by on one side of the equation. To do this, you need to eliminate the ax term from the left side. This can be achieved by subtracting ax from both sides of the equation. This is based on the fundamental principle that performing the same operation on both sides of an equation maintains equality.
- Original equation: ax + by = c
- Subtract ax from both sides: ax + by - ax = c - ax
- Simplified equation: by = c - ax
-
Divide by 'y': Now that you have isolated the term by, the next step is to isolate 'b' itself. Since 'b' is multiplied by 'y', you can isolate 'b' by dividing both sides of the equation by 'y'. Again, this maintains the equality of the equation. It's important to note that this step is only valid if y is not equal to zero. If y is zero, the equation becomes ax = c, and 'b' disappears from the equation.
- Equation: by = c - ax
- Divide both sides by 'y': by / y = (c - ax) / y
- Simplified equation: b = (c - ax) / y
-
Simplify (if possible): The final step is to simplify the expression if possible. The equation b = (c - ax) / y is the solution for 'b', but it can sometimes be further simplified depending on the specific values of a, c, x, and y. For example, if c and ax have a common factor, you can simplify the numerator before dividing by y.
- Solution: b = (c - ax) / y
- Depending on the values of a, c, x, and y, further simplification might be possible.
Illustrative Examples: Putting Theory into Practice
Let's solidify our understanding with a few practical examples:
-
Example 1: Solve for 'b' in the equation 2x + 3b = 9
- Step 1: Subtract 2x from both sides: 3b = 9 - 2x
- Step 2: Divide both sides by 3: b = (9 - 2x) / 3
- Simplified solution: b = 3 - (2/3)x
-
Example 2: Solve for 'b' in the equation 5x + by = 20, given that x = 2 and y = 4
- Step 1: Substitute x = 2 into the equation: 5(2) + by = 20
- Simplify: 10 + by = 20
- Step 2: Subtract 10 from both sides: by = 10
- Step 3: Substitute y = 4 into the equation: 4b = 10
- Step 4: Divide both sides by 4: b = 10 / 4
- Simplified solution: b = 5/2 = 2.5
-
Example 3: Solve for 'b' in the equation -3x - 2by = 12
- Step 1: Add 3x to both sides: -2by = 12 + 3x
- Step 2: Divide both sides by -2y: b = (12 + 3x) / (-2y)
- Simplified solution: b = -(12 + 3x) / (2y) or b = (-6 - (3/2)x)/y
Potential Pitfalls and How to Avoid Them
When solving for 'b', there are several common mistakes to watch out for:
-
Dividing by Zero: As mentioned earlier, you cannot divide by zero. If the coefficient 'y' is zero, the equation is no longer solvable for 'b' in the same manner. Instead, the original equation simplifies to ax = c, and the relationship between 'a', 'x', and 'c' becomes the focus. This situation indicates that 'b' is not a relevant factor in the equation's solution.
-
Incorrect Order of Operations: Always follow the correct order of operations (PEMDAS/BODMAS – Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction). Make sure to isolate terms properly before dividing or multiplying. Failing to do so can lead to incorrect results.
-
Sign Errors: Pay close attention to signs (positive and negative). A simple sign error can completely change the outcome of the equation. Double-check each step to ensure that signs are correctly applied when adding, subtracting, multiplying, or dividing.
-
Forgetting to Apply Operations to Both Sides: The golden rule of algebra is that any operation performed on one side of the equation must be performed on the other side to maintain equality. Forgetting to do this will result in an unbalanced equation and an incorrect solution.
Real-World Applications: Where Solving for 'b' Comes in Handy
While manipulating equations might seem like a purely academic exercise, it has countless real-world applications. Here are a few examples:
-
Physics: In physics, many equations relate different physical quantities. For instance, the equation relating distance, initial velocity, time, and acceleration can be rearranged to solve for a specific variable, such as acceleration.
-
Engineering: Engineers often use linear equations to model circuits, structures, and systems. Being able to solve for a particular parameter, like resistance in a circuit, is essential for design and analysis.
-
Economics: Economic models often involve linear equations that describe relationships between variables like supply, demand, and price. Solving for a specific variable allows economists to analyze the impact of changes in other variables.
-
Computer Science: Linear equations are fundamental in computer graphics, optimization problems, and machine learning algorithms. Solving for specific variables is critical for manipulating data and creating effective models.
-
Financial Analysis: Financial analysts use equations to calculate returns on investment, loan payments, and various financial metrics. Being able to isolate variables allows them to analyze different scenarios and make informed decisions.
Advanced Insights: Beyond the Basics
While the step-by-step method provides a solid foundation, here are some advanced insights to elevate your understanding:
-
Systems of Equations: Solving for 'b' in a single equation is a building block for solving systems of linear equations. Systems of equations involve multiple equations with multiple variables, and solving them often requires isolating variables in each equation and then combining the equations to find the values of all variables.
-
Matrices and Linear Algebra: In more advanced mathematics, linear equations are often represented using matrices. Linear algebra provides powerful tools for solving systems of equations using matrix operations, which are essential in fields like engineering, physics, and computer science.
-
Non-linear Equations: While this article focuses on linear equations, the principles of isolating variables are also applicable to non-linear equations. However, non-linear equations often require more complex techniques to solve, such as numerical methods or iterative approaches.
-
Graphical Representation: Linear equations can be represented graphically as straight lines. The slope and y-intercept of the line can be determined from the equation, and the solution to the equation can be interpreted as the point where the line intersects a particular value or another line. This graphical representation provides valuable insights into the behavior of the equation.
Tren & Perkembangan Terbaru
In recent years, the application of solving linear equations has expanded significantly due to advances in computing power and data analysis techniques.
-
Machine Learning: Linear algebra, including the manipulation and solution of linear equations, is a cornerstone of machine learning. From linear regression models to neural networks, these techniques rely heavily on the ability to solve for and optimize parameters within linear equations.
-
Big Data Analytics: As data sets grow larger, the need for efficient algorithms to process and analyze the data becomes increasingly important. Solving systems of linear equations is a crucial component of many data analysis techniques, enabling businesses and researchers to extract valuable insights from large datasets.
-
Optimization Algorithms: Many optimization problems can be formulated as linear programs, which involve solving systems of linear equations subject to certain constraints. These optimization algorithms are used in a wide range of applications, from supply chain management to resource allocation.
-
Quantum Computing: Quantum computers have the potential to solve certain linear algebra problems much faster than classical computers. As quantum computing technology matures, it could revolutionize fields that rely heavily on solving systems of linear equations, such as materials science and drug discovery.
Tips & Expert Advice
Here are some expert tips to help you master solving for 'b' in the equation ax + by = c:
-
Practice Regularly: The key to mastering any mathematical skill is practice. Work through numerous examples of varying difficulty to build your confidence and fluency. The more you practice, the more natural the process will become.
-
Break Down Complex Problems: If you encounter a complex problem, break it down into smaller, more manageable steps. Focus on isolating the term containing 'b' first, then proceed with dividing by 'y'. Breaking down the problem makes it less intimidating and reduces the likelihood of errors.
-
Check Your Work: Always check your work by substituting the solution back into the original equation to ensure that it satisfies the equation. This is a simple but effective way to catch errors and verify that your solution is correct.
-
Use Online Resources: Take advantage of the many online resources available, such as interactive calculators, video tutorials, and practice problems. These resources can provide additional support and guidance as you learn.
-
Seek Help When Needed: Don't be afraid to ask for help if you're struggling. Talk to your teacher, a tutor, or a classmate. Explaining your difficulties to someone else can often help you gain a new perspective and overcome your challenges.
FAQ (Frequently Asked Questions)
-
Q: What happens if 'y' is zero?
- A: If 'y' is zero, the equation becomes ax = c, and you cannot solve for 'b' in the same way.
-
Q: Can I solve for 'b' if 'a', 'x', and 'c' are unknown?
- A: No, you need at least numerical values or expressions for 'a', 'x', and 'c' to find a numerical value or expression for 'b'.
-
Q: Is there a different approach to solving for 'b'?
- A: The method described is the most straightforward. The core concept is always to isolate 'b' using inverse operations.
-
Q: Why is solving for variables so important?
- A: It's fundamental to algebra and allows you to analyze and manipulate equations in various fields.
-
Q: Can this be applied to more complex equations?
- A: The principle of isolating variables applies to many equations, though the specific steps may vary.
Conclusion
Mastering the skill of solving for 'b' in the equation ax + by = c is a fundamental stepping stone in algebra and beyond. By understanding the basic principles, following the step-by-step guide, practicing with examples, and being aware of common pitfalls, you can confidently tackle this type of equation and apply it to real-world problems. Remember to practice regularly, break down complex problems, check your work, and seek help when needed.
The ability to manipulate and solve for variables is a powerful tool that unlocks a deeper understanding of mathematical relationships and empowers you to solve a wide range of problems. Keep practicing, keep exploring, and continue to build your mathematical skills. How do you plan to use this new skill in your future studies or projects?
Latest Posts
Latest Posts
-
What Is The Role Of A Government
Nov 18, 2025
-
Hell Is Other People In French
Nov 18, 2025
-
The Bystander Effect Likely Occurs Due To
Nov 18, 2025
-
Arguments On The Existence Of God
Nov 18, 2025
-
What Was The Mapp V Ohio Case
Nov 18, 2025
Related Post
Thank you for visiting our website which covers about Solve For B Ax By C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.